Moment of inertia
Moment of inertia is the rotational analogue to mass. The mass moment of inertia about a fixed axis is the property of a body that measures the body's resistance to rotational acceleration. The greater its value, the greater the moment required to provide a given acceleration about a fixed pivot. The moment
of inertia must be specified with respect to a
chosen axis of rotation.
The symbols Ixx, Iyy and Izz are frequently used to express the moments of inertia of a 3D rigid body about its three axis.
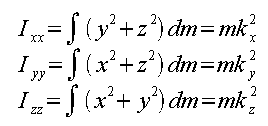 (A)
(A)Products of Inertia are given by Ixy, Ixz and Iyz where
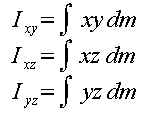 (B)
(B)Inertia Matrix
The moment of momentum, can be
expressed as
can be
expressed as 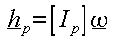 (C) (See PDF
for an explanation of how this is obtained)
(C) (See PDF
for an explanation of how this is obtained)Where
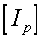 is the Inertia Matrix
is the Inertia Matrix 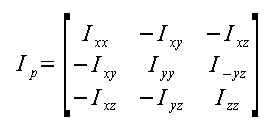
Problems where the moment of momentum vector, h is parallel to
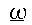 are easier to
solve, so the moment of momentum can be expressed as
are easier to
solve, so the moment of momentum can be expressed as 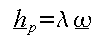
If this expression for is substituted into equation (C) then the following expression is obtained.
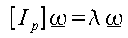
This can be seen to be an eigenvalue problem, the three eigenvalues
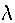 of
of 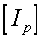 define the axis about which the body can spin maintaining h
parallel to
define the axis about which the body can spin maintaining h
parallel to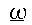
The three eigenvalues are the principle moments of inertia and are known as A B and C
The three eigenvectors are the principle axis of inertia and are orthogonal.
When the axis are aligned with the principle axis Ip can be expressed as
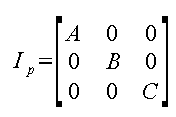
Therefore axis aligned with principle are useful in solving practical problems
Moments of Inertia of a gyroscope
A gyroscope is an axisymmetric body
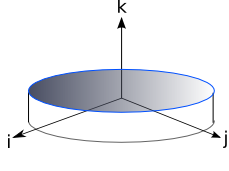
Due to the axisymmetry of a gyroscope all axis in the i-j plane are principle. A gyroscope can be thought of as an AAC body. It has principle moments of inertia A A and C