In 1687 Isaac Newton presented three laws on the motion of a particle. It is these laws which in his Royal Institution lecture Eric Laithwaite claimed only applied to motion in straight lines and where there is no net acceleration.
Newton's Laws of motion can be stated as:
First Law: A particle at rest, or moving in a straight line will remain in this state provided the particle is not subject to an unbalanced force.
Second Law:
A particle acted upon by an unbalanced force F experiences an
acceleration a
that has same direction as the force and a magnitude that is directly
proportional to the force (this can be interpreted as 'F=ma' where m is the
mass of the particle).
Third Law: The mutual forces of action and reaction between two particles are equal, opposite and collinear.
Newton's laws of motion applied to a body
Newton's Laws are related to the motion of a particle, however, in the context of gyroscopic motion such as that demonstrated in Laithwaite's lecture the motion of whole bodies is dealt with. Any 'body' is a collection of particles, therefore, by summing over all the particles in a body we can see how Newton's Laws relate to bodies.The key result of this
analysis is that 'F=ma' holds for any
rigid body provided it is applied to the center of mass
rigid body provided it is applied to the center of mass
Newton's laws of motion applied to circular motion
A gyroscope is essentially a mass that spins at a high rate about its axis of symmetry, mounted so this axis of rotation can change. Therefore, an analysis of a general body can be carried out which takes account of angular motion in 3D. The following result is found: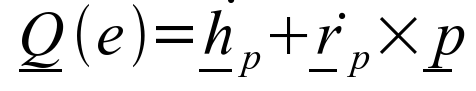
This is derived from Newton's Second Law and applies to angular motion of 3-D rigid bodies. This result is used in the repetition and analysis of Laithwaite's videos, and can be seen to hold for all cases. Laithwaite claimed that Newton's Laws of motion do not hold for circular motion, but there is some other force acting. This is not the case, Newton's Second Law, which applies to the motion of a particle can be used to obtain the above formula which holds for circular motion.