 and for other stuff: go to
Hugh Hunt's home page )
and for other stuff: go to
Hugh Hunt's home page )( Gyroscopes and Boomerangs: go to
Hugh Hunt's gyro and boomerang page
 and for other stuff: go to
Hugh Hunt's home page )
and for other stuff: go to
Hugh Hunt's home page )
This site contains several movies that illustrate the dynamics of spin. Dynamics is a boring subject without spin:
a translating body does nothing interesting, and an ideal particle behaves much as you would expect. Some of the
phenomena illustrated below are very complicated to understand, but very easy to observe. I hope these videos will help
to open a few eyes to the wonders of spin.
If you have trouble viewing the videos then go to
testpage or download RealPlayer.V.10
Ball bouncing under a table
(MPG) or
(CIN) or
 (AVI) and a simulation
(MPG) or
(CIN) or
(AVI) and a simulation
(MPG) or
(CIN) or
 (AVI)
(AVI)
 Note that the ball comes back from where it came
Note that the ball comes back from where it came

Note the spin of the ball and that it exits without spin in the direction that it entered.
Isn't it extraordinary that the ball returns almost exactly along its entry path? A light beam certainly wouldn't
do this, so strengthening the case for exercising caution when referring to the "particle theory of light". The particle
theory of light assumes that the particle has mass but no moment of inertia and that it has no physical size. I've never
seen a ball in the playground that fits this description!
 Lambard's non-goal popped back to the keeper because of spin - to find out why, click here .
Lambard's non-goal popped back to the keeper because of spin - to find out why, click here .
(MPG) or
(CIN) or
 (AVI)
(AVI)

Note that the exit angle is not equal to the entry angle, and note the spin.
It is for this reason that I object to the "particle theory of light" being taught in schools without some kind
of clear indication that superballs (or any ball for that matter) do not behave as particles. How can kids be expected
to understand the particle theory of light if experiments that they can easily perform
with "particles" in the playground demonstrate that particles don't behave as
light does?
Downball - Simulation of a ball bouncing against a wall, hitting the floor first
(MPG) or
(CIN) or
 (AVI)
(AVI)

Note now that the exit angle is yet again different
from the entry angle. If the particle were to behave as if it were a beam of light then the exit path would be
parallel to the entry path. But then ball games in the playground wouldn't be nearly as much fun without spin!
 (AVI) and a simulation
(MPG) or
(CIN) or
(AVI) and a simulation
(MPG) or
(CIN) or
 (AVI)
(AVI)
 Note that the ball doesn't just bounce back - it jumps in the air
Note that the ball doesn't just bounce back - it jumps in the air
 DRY WALL
DRY WALL
The upward force that causes the ball to jump also causes the spin direction to reverse. This reversal of spin is exactly what
is needed for the ball ultimately to begin rolling back the other way.
Now if we assume that the wall is slippery, then the ball cannot be lifted up into the air. As a result there is no force from the wall
to change the direction of spin so the ball begins its return journey spinning the wrong way. Friction with the floor
gradually acts to reverse the spin direction, but
this friction force also slows the ball down and in the process the ball is almost brought to a complete halt.
 (AVI)
... but now with a slippery wall the ball doesn't jump up
(AVI)
... but now with a slippery wall the ball doesn't jump up
 OILY WALL
OILY WALL
This is completely counterintuitive - who'd have thought that lubricating the wall would cause the ball to bounce back more slowly?
(MPG) or
(CIN) or
 (AVI)
- this is a top view.
(AVI)
- this is a top view.

Note that the ball does not reflect at 45 degrees. It is airborne and then it changes direction after the first bounce. Note also the change in spin as it bounces.
The videos below give three examples, two steady-state limit cycles and one example of chaotic motion.
The limit cycles are very special circumstances that arise given particular intial conditions. Chaos is the usual situation.
In any case, the simulations are very-much idealised and any experiemnt will do diferent things yet again. This is the nature
of non-linear systems and chaotic motion. The world is full of non-linear phenomena so how can we expect to model it accurately?
We can only ever hope to scratch the surface.
(the AVI videos show the full development of steady state whereas the mini animations show a small steady-state snapshot
of the motion. The JPG links show the motion graphically)
 (AVI)
- ball on bat in a simple limit cycle
- note the ball hits the bat once per cycle
(AVI)
- ball on bat in a simple limit cycle
- note the ball hits the bat once per cycle
 (JPG)
(JPG)
 (AVI)
- ball on bat in a complex limit cycle
- the bat oscillates at twice the ball bounce rate and the ball height alternates
(AVI)
- ball on bat in a complex limit cycle
- the bat oscillates at twice the ball bounce rate and the ball height alternates
 (JPG)
(JPG)
 (AVI)
- ball on bat in chaotic motion
- this is the usual condition.
(AVI)
- ball on bat in chaotic motion
- this is the usual condition.
 (JPG)
(JPG)
Modelling is difficult for three reasons:
1 - The impact is hard to model. Most people use "coefficient of restitution" and this is a simplistic approach.
But there are not many alternatives! I have used a coefficient of restitution e=0.9 for all the animations here. The biggest concern
is that impact is assumed to be instantaneous - which it isn't. A more-realsitic model has to include a spring at the contact
interface and this spring may itself be non-linear and dissipative.
2 - Even for a simple ball with a single contact point bouncing on a sinusoidally-moving table the problem is nonlinear and chaotic
solutions result. Solving such systems is not for the feint-hearted.
3 - Being a non-linear and chaotic system it is very sensitive to the method of modelling and also sensitive to initial conditions.
Then when it comes to modelling more realistic problems (for instance an object bouncing in the back of a truck on a bumpy road)
it is necessary to include multiple contacts and these add significant complexities and uncertainties.
The Matlab code used to generate this bat-on-ball motion can be found here . This code comes with no guarantees.
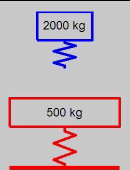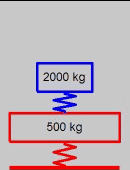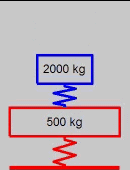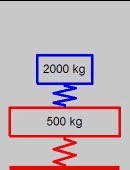 (AVI)
- two-mass impact problem
(AVI)
- two-mass impact problem
 (JPG)
(JPG)
The Matlab code used to generate the motion shown can be found here . This code comes with no guarantees.
 (AVI)
- chaotic motion of a double pendulum
- the motion is unpredictable
(AVI)
- chaotic motion of a double pendulum
- the motion is unpredictable
 (JPG)
(JPG)
The obvious question to ask is "how can the motion be modelled yet at the same time be unpredictable"? It is true that I have made a mathematical model and I have simulated the motion to produce the animation here. But if an experiment were performed the observed motion would not be the same as the prediction here. This is because the initial conditions used in the simulation cannot be exactly the same as those in an experiment. Also the presence of small deviations from "ideal behaviour", for instance friction or perhaps flexibility of the bearings, or lack of rigidity of the pendulum rod etc. etc. will lead to massive deviations from the model predictions.
The Matlab code used to generate this chaotic doublependulum motion can be found here . This code comes with no guarantees.

|
Toast always seems to land buttered-side down when you drop it.
|
(these make excellent exam questions)
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
These movies show the classic and counter-intuitive motion of a ball rolling without slip on a horizontal rotating turntable. Note that the ball moves on a space-fixed circle whose centre and radius are determined solely by initial conditions. The period of motion of the ball on its circle is 7/2 that of the table (5/2 for a hollow sphere, eg a ping-pong ball). These results are independent of the size and mass of the ball. If the table is sloping then the centre of the ball convects with a constant velocity perpendicular to the slope as shown in the last of the movies.
(for an analysis, see ball-on-turntable analysis
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
This shows the beautiful motion of a ball rolling without slip inside a fixed cylindrical shell. The period of up-and-down motion of the ball is sqrt(7/2) that of the orbiting period, independent of the size and mass of the ball. The amplitude of up-and-down motion depends on initial conditions and, as the video shows, it is possible to cause the ball to leave the cylinder. The best kind of ball to use is a rubber-coated steel ball (ie a mouse ball).
(for an analysis, see ball-in-cylinder analysis)
(MPG) or
(CIN) or
These videos show the motion of a ring wobbling down a rod. These derive from the study of a toy known variously as a gyro ring (gyroring gyro-ring),
a wobble ring or a jitter max. There are two motions, one with a single contact point and another with two contact points.
The two-contact-point motion is exhibited in the toys, but the single-contact-point motion is quite beautiful and counter-intuitive- only observed with thin rings.
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(for a geometric interpretation of this motion involving momental and energetic ellipsoids, see momental ellipsoids for a tumbling rigid-body)
The motion is governed by conservation laws (kinetic energy and moment of momentum). These laws are simple but solution
of the equations of motion (Euler's equations) is tricky, involving Jacobian Elliptic Functions. Matlab has been used to
procuce the following simulated motions:
(MPG) or
(CIN) or
(MPG) or
(CIN) or
(MPG) or
(CIN) or
This popular game is played with a ball on a string attached to a vertical pole. Two players with bats attempt
to out-do each other, one playing clockwise and the other anti-clockwise. Here is a photo of children playing
swingball kids playing swingball
The motion of the ball is governed by two conservation laws:
(MPG) or
(CIN) or
(MPG) or
(CIN) or
Equations of Motion
- are given here. The equations are simple, but the solution is tricky.
Mysterious rigid-body motions are exhibited by boat-shaped object spun on a flat surface. Smooth river-worn stones also show this motion. A given object will have a preferred direction of spin.
Rattlebacks are also known as "wobblestones" or "celts".
(MPG) or
(CIN) or
(MPG) or
There's some really nice mechanics involved with falling chains. It is possible to make a chain fall to the ground faster than g=9.81m/s2 .
Don't believe me? Take a look at
Andy Ruina's stuff
Andy also drew my attention to this amazing video
"Fishing under ice"
from Finland. Who would believe you can pour air out of a wheelbarrow?
This program is useful for demonstrating the importance of visualizing and modelling the essential mechanics of
motion - by example of an exercise machine.
(EXE)
- An exercise machine
Gabor Domokos and his
Gömböc -
as featured on the BBC "quiz" show QI, Fri 13 February 2009. You need to go about half way through (13m30s).
Best viewed in RealPlayer, but it has also been known to work in Windows Media Player.
(WMV)
This page contains low-resolution animated GIFs which should play automatically.
To view the video full-size then click on the
MPG ,
CIN or
AVI links,
choosing the one that plays best on your computer.
If you're having trouble viewing the full-size
videos then please go to
testpage .
last update 20 October 2011
Pencils
 (AVI)
- Pencil falling onto the edge of a table
(AVI)
- Pencil falling onto the edge of a table
 - note that the pencil loses some of its energy on collision
- note that the pencil loses some of its energy on collision
 (AVI)
- Pencil hit off the edge of a table - just hits
(AVI)
- Pencil hit off the edge of a table - just hits

 (AVI)
- Pencil hit off the edge of a table - just misses
(AVI)
- Pencil hit off the edge of a table - just misses

Ball rolling on a rotating table
 (AVI)
(AVI)
Ball moving on a circle centred on the centre of the table
 (AVI)
(AVI)

Ball moving on a small circle centred some way off the table centre>
 (AVI)
(AVI)

Ball stationary (ie a circle of zero radius)
 (AVI)
(AVI)

Ball rolling on a larger circle passing through the table centre
 (AVI)
(AVI)
 - Ball rolling on a sloping table
- Ball rolling on a sloping table
Because this is a big video you may have trouble downloading it. It has to be big in order to
show the ball rolling on the sloping table before being spun up, then to show the spinup, then
showing the remarkable convection at 90 degrees to the expected direction.
Here is a smaller version:
(AVI)
Provided that you trust that the slope of the
table in the following two clips is the same, then these files are smaller and just as remarkable.
 Ball on sloping table, table not spinning (AVI) or
(MPG)
or
(CIN)
Ball on sloping table, table not spinning (AVI) or
(MPG)
or
(CIN)
 Ball on sloping table, table is now spinning (AVI) or
(MPG)
or
(CIN)
Ball on sloping table, table is now spinning (AVI) or
(MPG)
or
(CIN)
Ball rolling inside a cylinder
 (AVI)
- Ball moving inside a circular cylinder
(AVI)
- Ball moving inside a circular cylinder

Wobblerings
 (AVI)
- Single-contact-point motion
(AVI)
- Single-contact-point motion
 - note the beautiful up-and-down bouncing motion
- note the beautiful up-and-down bouncing motion
 (AVI)
(AVI)
 - Double-contact-point motion
- note that the motion is very fast compared with single-point motion
- Double-contact-point motion
- note that the motion is very fast compared with single-point motion
 (AVI)
(AVI)

Single-contact motion on a horizontal rod
- motion on a horizontal rod removes the effect of gravitationally-induced slip convection
(MPG) or
(CIN) or
 (AVI)
- Double-contact motion on a horizontal rod
(AVI)
- Double-contact motion on a horizontal rod

 (AVI)
- Two-contact-point motion for a ring moving down a rod
(AVI)
- Two-contact-point motion for a ring moving down a rod

 (AVI)
- The same motion, but viewed from above
(AVI)
- The same motion, but viewed from above
 - note that it looks as if the ring makes a "flip", but this is an illusion resulting from the camera angle. The motion is in fact steady
- note that it looks as if the ring makes a "flip", but this is an illusion resulting from the camera angle. The motion is in fact steady
 (AVI)
(AVI)

The toy, showing normal two-contact-point motion of five rings
 (AVI)
- A closeup slow-motion of the toy
(AVI)
- A closeup slow-motion of the toy
Stability of a rigid body spining freely in space
(MPG) or
(CIN) or
 (AVI)
- The classic unsteady motion of a rigid body about the intermediate moment of inertia
(AVI)
- The classic unsteady motion of a rigid body about the intermediate moment of inertia

 (AVI)
- Spin about the "A" axis( stable)
(AVI)
- Spin about the "A" axis( stable)

 (AVI)
- Spin about the "B" axis (unstable)
(AVI)
- Spin about the "B" axis (unstable)

 (AVI)
- Spin about the "C" axis( stable)
(AVI)
- Spin about the "C" axis( stable)

Swingball (Totem tennis)
 (AVI)
- a "gentle" hit which doesn't go over the head of your opponent
(AVI)
- a "gentle" hit which doesn't go over the head of your opponent

 (AVI)
- a "smash" which goes over the head of your opponent - this is aggressive play!
(AVI)
- a "smash" which goes over the head of your opponent - this is aggressive play!

Rattlebacks
 (AVI)
- A home-made rattleback
(AVI)
- A home-made rattleback


 (AVI)
- Another pair of home-made rattlebacks
(AVI)
- Another pair of home-made rattlebacks


 This shows how pretty-much any household object can be turned into a rattleback!
This shows how pretty-much any household object can be turned into a rattleback!

Falling Chain
 (MPG) or
(MOV) at Cornell. He does neat things with
bikes
as well
(MPG) or
(MOV) at Cornell. He does neat things with
bikes
as well
Kinematics
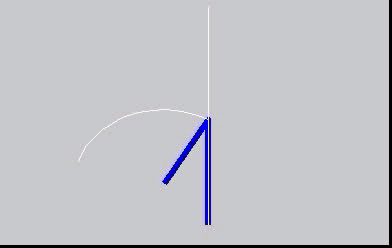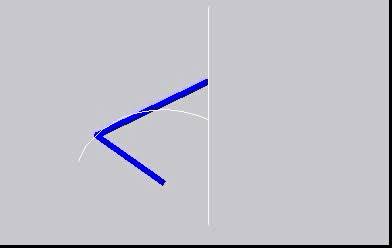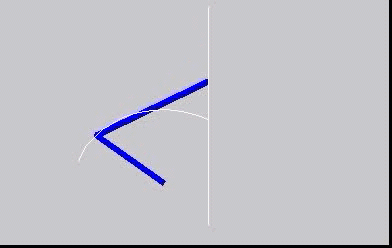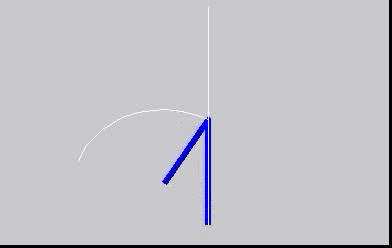
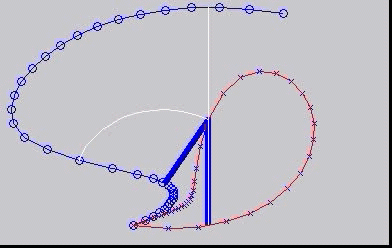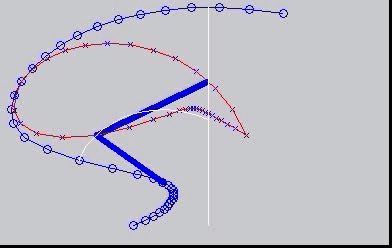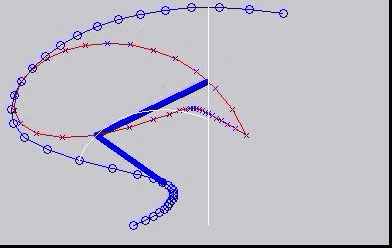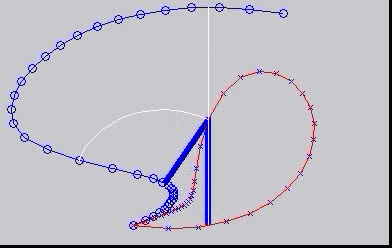
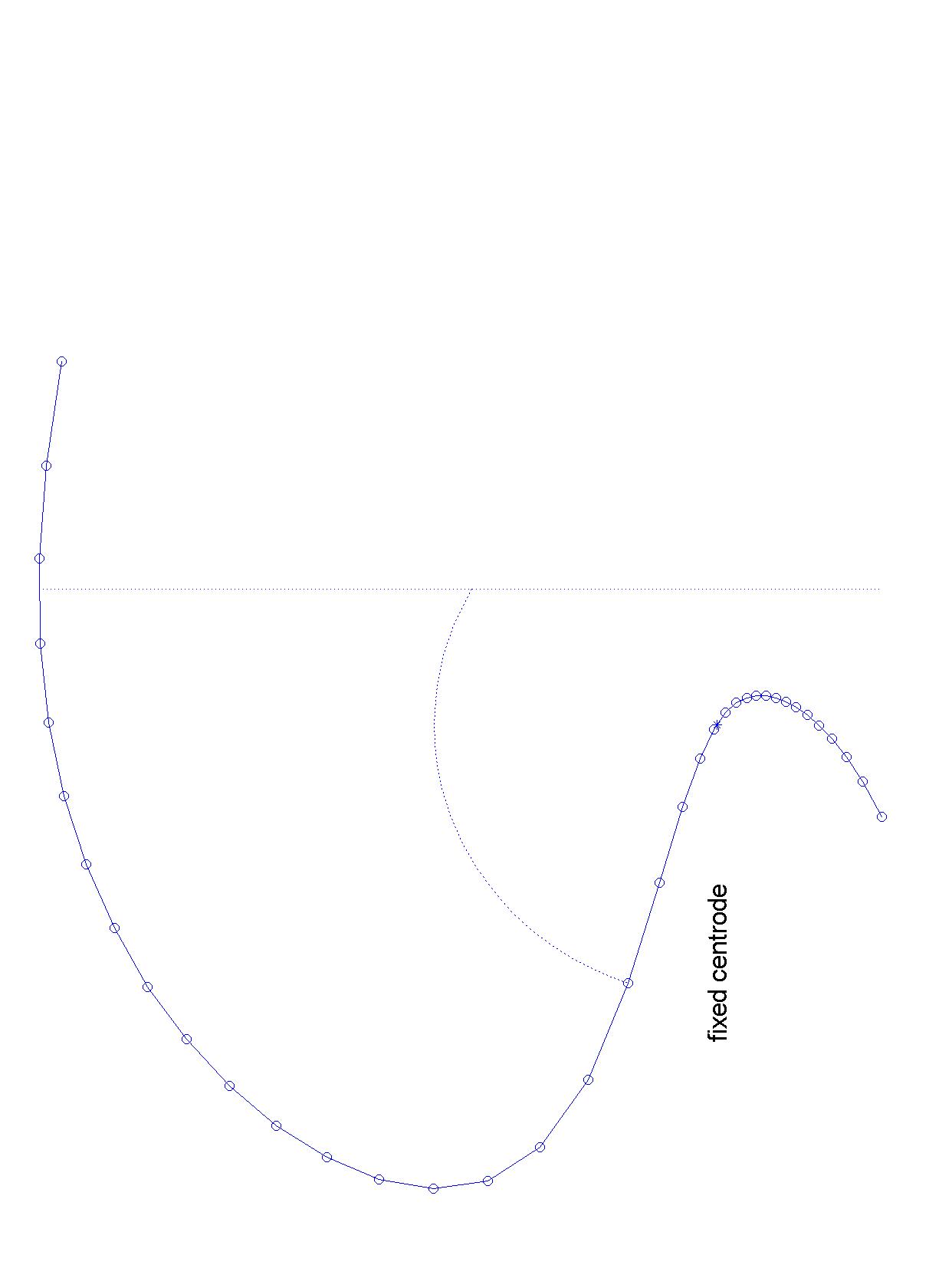
Instantaneous centres - centrodes
The concept of instantaneous centres is illustrated here, with the moving centrode rolling without slip on the fixed centrode.
This is a simple mechanism: The blue bars are the mechanism, with a crank (rotating about a fixed point) connected to a follower with
its other end moving as a slider along a straight line. The beautiful thing is that the motion of the follower can be reproduced exactly
by the two rather strange shaped 'centrodes' rolling on each other. This is the subject of "kinematic geometry".
 Do it yourself with these images for printing:
Do it yourself with these images for printing:

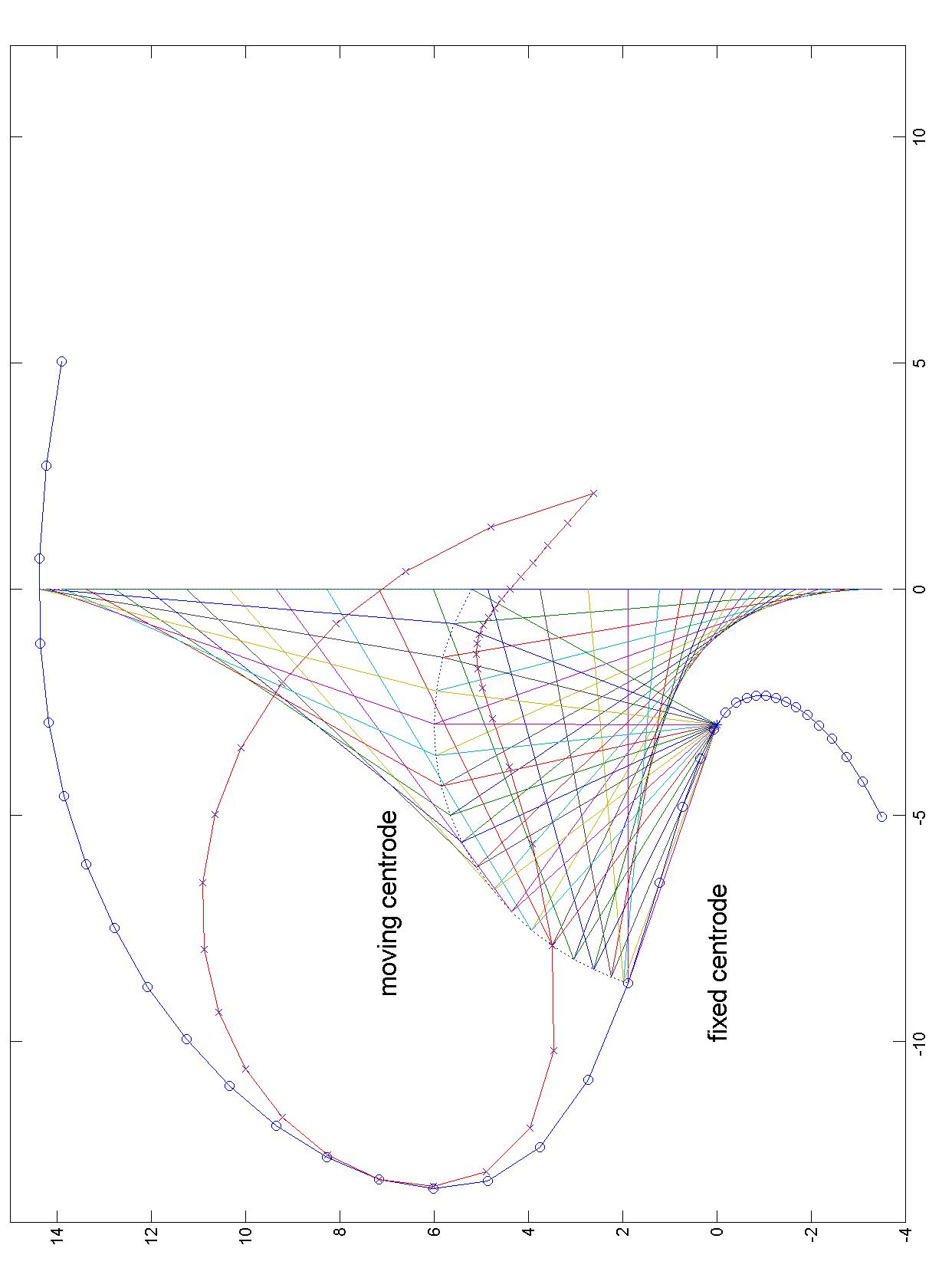 matlab code
matlab code
Gömböc
If you make use of these, please acknowledge their source.
I acknowledge the help and support of the following people:
Prof Mark Warner (Cavendish Labs Cambridge)
, Dr Paul Robertson and Dr Sue Jackson (Multimedia Group, CUED)
, David Miller and the team (Frank, Gareth, Chris, Len, Gary) (CUED Mechanics Lab)
, Prof Gareth McKinley, Prof Doug Hart, Pierce Hayward, Sean Buhrmester (MIT Mech Eng)
, Emma Wilson (CUED)
hemh1 (at) cam.ac.uk
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(
)