Instability of a rigid body
spinning freely in space
Hugh Hunt, Cambridge University
(movies on this subject are here)
A rigid body spinning in space conserves kinetic energy T and moment of momentum H. Expressions for the two are T=½(A w12 + Bw22 + Cw32) = const1, and H=Aw1i + Bw2j + Cw3k = const2 (a vector constant in magnitude and direction). The reference frame i, j, k is body-fixed, so as the body rotates the direction of H is not constant in this frame. However the magnitude of H must be constant, giving H=Ö(A2 w12 + B2w22 + C2w32) = const2. Plotting constancy of T and H using w1 w2 and w3 as ordinates gives two ellipsoids. The only allowable spinning states are at their intersections.
Here is an example in which the momental ellipsoid is shown green/yellow/orange and the energy ellipsoid is blue/white. The black line represents the intersection of the two ellipsoids, ie the allowable states, showing that spin near the ‘B’ axis is a ‘saddle’ and is unstable. You can check this by spinning a book, a tennis racquet, a cellphone … anything really, and noticing that it will not spin stably about the axis of its intermediate moment of inertia. Spin about the other two axes is stable.
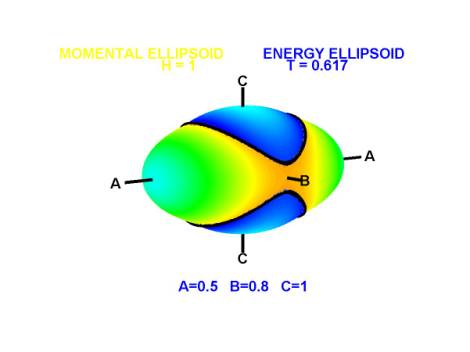
To get a more complete picture, the momental ellipsoid shown below is marked with the intersection lines of the energy ellipsoid for all possible spins, the blue line being for spin about the ‘A’ axis (or close thereto), the white being for spin about the ‘C’ axis – and note that both of these are stable. The saddle for spin about ‘B’ is the red line. (note: the colour coding of the ellipsoid is not important – it is only intended to help give a 3D effect)
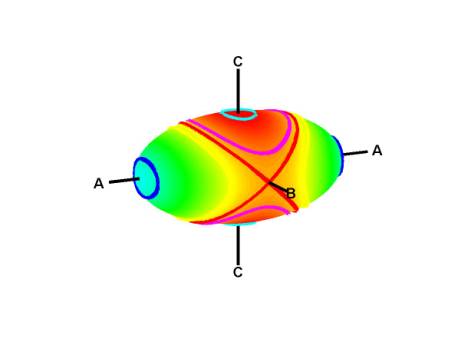
But spin about the ‘A’ axis is not really stable because of energy dissipation effects. For a given moment of momentum H, the highest energy state is spin about the ‘A’ axis (the blue line). Let us suppose that we spin the body about axis ‘A’. It is possible to envisage that as energy is lost within a spinning body (due to internal friction, say) then the trajectory will gradually ‘spiral’ around the surface of the ellipsoid, all the while conserving angular momentum H but losing energy T. The spin will appear rather ‘wobbly’ as the body gradually settles down to spin about the lowest-energy state, about the ‘C’ axis. There is no more energy to lose now.
You can try this too. Take an object that will dissipate energy internally, for instance a key wallet or a bag of frozen peas. Spin this about any axis and it will quickly make its way to spinning about the axis with largest moment of inertia – ie the minimum-energy state.
Home: www.eng.cam.ac.uk/~hemh